Songwan's blog

s

알림

이 포스팅은 2019년 Harvard STAT115강의를 요약한 것임을 알려드립니다.

다룰 토픽

• Differential expression : Fold change, T* test on normally distributed data, empirical Bayes method
• Multiple test adjustment : FWER, FDR

Heatmap : Expression level visualization

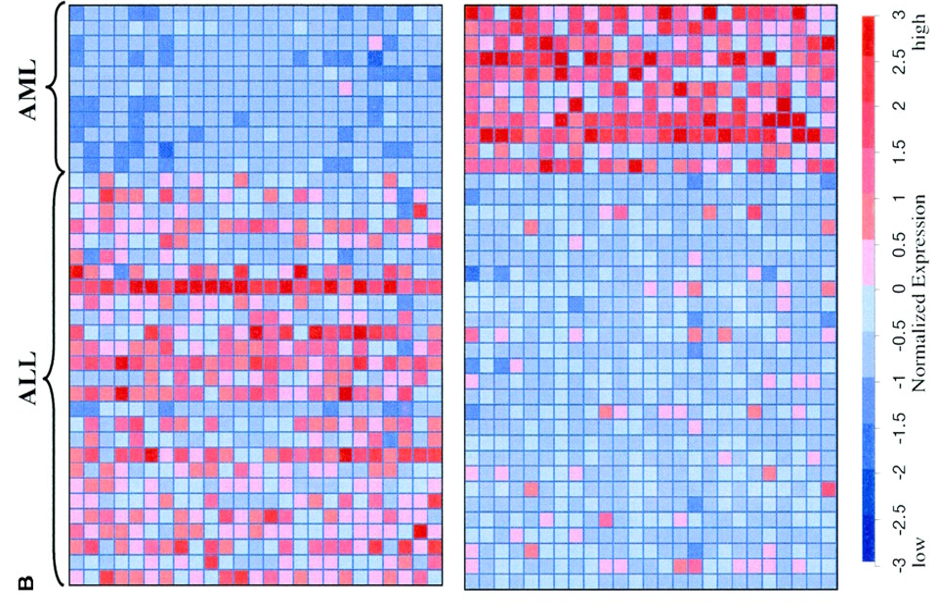
다음 그림은 암의 종류 (ALL, AMLL)에 따른 gene expression level을 그림으로 나타낸 것이다. 각 행은 gene을, 열은 sample을 의미하며, 빨간색으로 갈 수록 expression level이 높고, 파란색으로 갈 수록 expression level이 낮다고 볼 수 있다. 주의해야 할 점은 row의 ordering이 매우 중요하다는 것이다. 어떻게 ordering을 하느냐에 따라 visualization이 매우 달라질 수 있다.

어떻게 우리는 Differential expression의 정도를 계산할까?

1) Fold change (Avg(X) / Avg(Y))를 사용하는 것 (Naive method)

• MAS4, MAS5, dChip

  • Natural scale을 사용하므로 바로 fold change 계산

• RMA를 사용하는 방법 (microarray 포스팅 참고)

  • RMA는 log scale을 사용하기 때문에 샘플 X와 sample Y의 평균 expression level을 빼면 log(Avg(X)) - log(Avg(Y)) = log(Avg(X)/Avg(Y))이다. 따라서 fold change (Avg(X) / Avg(Y))를 계산하려면 두 로그값의 차이에 exponential을 취해주어야 한다. 그렇지 않으면 geometric mean을 게산한 것이 된다.

• 예시 : 다음과 같이 Gene 1, 2와 Gene 3에 대한 3개의 Treatment sample (T1, T2, T3), 3개의 Control sample (C1, C2, C3)와 Fold change 값 (FC)가 있다고 하자.

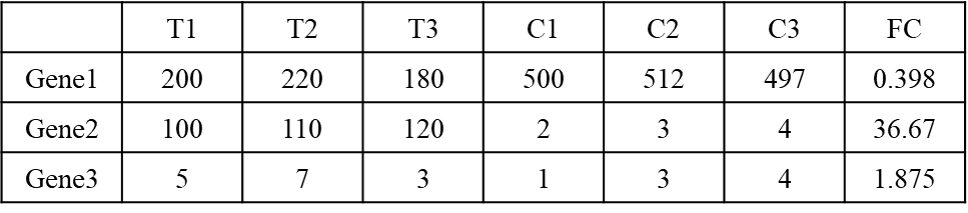
• FC = 36.67은 Treatment group에서 크게 overexpressed된 것을 알 수 있고, FC = 1.875은 Treatment group에서 약간 overexpressed된 것을 알 수 있다.
• 다른 예시를 보자.

• Gene 4를 보면 Control보다 Treatment에서 더 높은 값을 가짐을 알 수 있다. 반면 Gene 5에서는 Control과 Treatment에 따른 차이가 크지 않다. 하지만 FC값은 2.213으로 동일하다. 여기서 Fold change사용의 문제점이 드러난다. 따라서, differential expression level의 confidence를 줄 수 있는 다른 통계량이 필요하다.

2) T-test (데이터가 정규분포를 따르는 경우)

• T-test는 데이터가 Normal을 따른다는 가정이 필요하다.
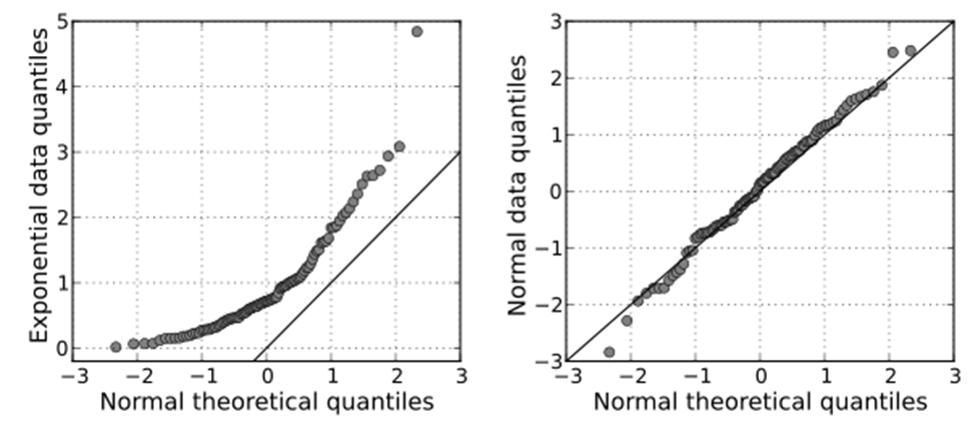
• 우선, 데이터가 Normality assumption을 만족하는지 알아보기 위해 QQ Plot을 그린다.

3) Wilcoxon Rank Sum Test (데이터가 정규분포를 따르지 않는 경우)

• 행에 있는 모든 데이터에 순위를 매긴후, Treatment와 Control그룹의 랭크의 합을 각각 $T_T$ 와 $T_C$라 하자.
• 예) 10개의 normal sample (control) 과 10개의 cancer sample (treatment)이 있다고 하면, min(T) = 55 ( = 1 + 2 + … + 10)이고 max(T) = 155 ( = 11 + 12 + … + 20)이다.
• Significance rule은 permutation에 의해 결정되는데, 예를 들어 위의 예시의 경우, 랜덤으로 많은 수의 조합 (permutation)을 simulation해서 분포를 그려보면 다음과 같다.

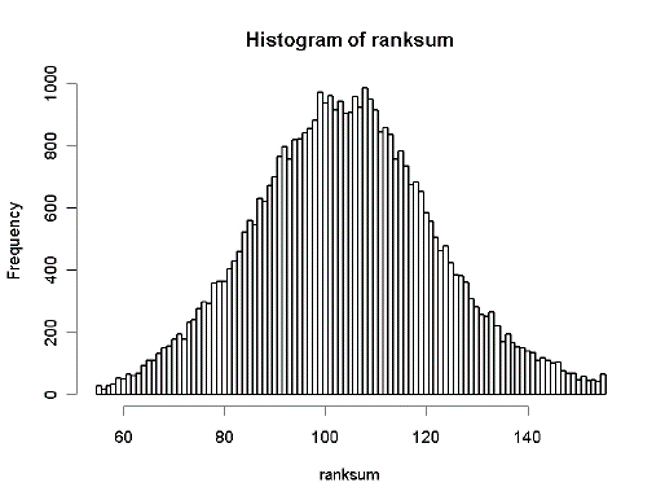
• 이 경우, T = 150 이상일 경우에 Significant하다고 할 수 있다. 여기서 150이라는 숫자는 U table (transformation of T)에서 도출할 수 있다.
• 하지만 이 방법은 nonparametric한 방법이므로, 샘플의 수가 적을 땨에는 power이 작다는 단점이 있다.

Linear Model for Differential Expression

• Linear model : $Y_{ijk} = \mu_{j} + \alpha_{ij} + error_{ijk}$ 은 각 gene j마다의 seperate한 linear model로써,

  • $k$ : 특정 sample
  • $Y_{ijk}$ : RMA analysis를 통한 expression index
  • $\mu_{j}$ : baseline gene expression level, gene j의 전체 experiment (RMA expression index)에 대한 평균 expression level
  • $\alpha_{ij}$ : differential expression from i-th condition, i-th condition의 overall mean ($\sum_{i}\alpha_{ij}=0$)으로부터의 편차(deviation)

• 이 모델에서, 3개의 treatment (mutant)와 3개의 control (wildtype)에 대해,
• 귀무가설 $H_0$ : $\alpha_{mu}$ - $\alpha_{widetype}$ $= 0$에대해 검정한다 (treatment와 control group사이에 차이가 있는가?)

1) Ordinary t-tests

• 일반적인 t-test는 다음과 같다.
• $$t_{g} = \frac{\bar{y}_{mutant}-\bar{y}_{wildtype}}{s_{g}c}$$
• where $c = \sqrt{\frac{1}{n_1}+\frac{1}{n_2}}$
• 여기서 c는 test statistic $t_g$의 인자로서, sample size에 영향을 받는다. 이는 당연한 것인데, confidence는 sample size에 영향을 받기 때문이다.
• 그렇다면 표준 편차인 $s_g$는 어떻게 계산할까?: 다음의 수식으로 계산할 수 있다. (여기서 $s_p$는 pooled sd)

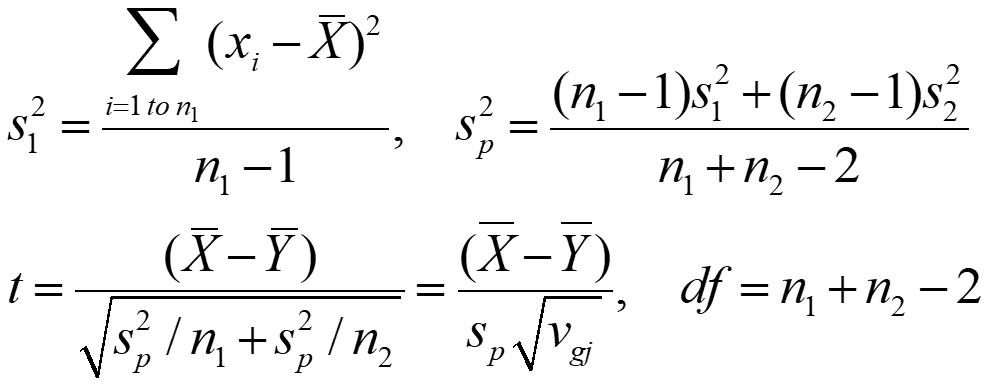
2) Welch-t test

• condition 별로 variance가 다른경우에 사용한다.
• $$t = \frac{(\bar{X} - \bar{Y})}{\sqrt{s_{1}^{2}/n_{1} + s_{2}^{2}/n_{2}}}$$

문제점

• 1)과 2)의 parametric한 방법은 sample size가 10은 넘어야 한다. 하지만, 위의 예시에서 3개의 treatment와 3개의 control replicate가 있는 경우, sample size가 너무 작다.
• 또한, replicate의 경우 서로간의 유사성이 높아 $s_g$가 매우 작을 가능성이 있다. 그러면 $t$의 값이 너무 커지므로 문제가 발생한다.

Variance Stabilization

• Statistical Analysis of Microarrays (SAM)

  • Modified t*를 사용함
  • $s_g$가 너무 작거나 0이 되는 것을 방지하기 위해, $s_g$를 다른 array로부터의 gene의 $s_g$를 사용해 증가시킴. (예: lowest 5 percentile of $s_g$값으로 대체하기)

• LIMMA algorithm, Smyth 2004 (SKIP, 다음에 다시 하기)

  • Empirical Bayes 방법을 사용함. 모든 gene으로부터 information을 borrow하는 것.

Multiple Hypothesis Testing

기존의 Differential expression analysis는 fold change가 2이상이거나 1.5이상이면 두 control과 treatment그룹의 gene expression level이 유의하게 차이가 난다고 하는 등 대략적인 기준을 많이 사용해왔다. 하지만, 다음과 같은 상황을 가정해보자.

• $H_0$ : trt와 ctr간 expression에 차이가 없음, $H_1$ : trt와 ctr간 expression에 차이가 있음
• $H_0$의 기각 : 차이가 있다고 생각되어지는 gene이 call됨
• 모든 gene에 대해 differential expression을 test한다. 이때 p-value < 0.01이면 control과 treatment그룹간의 차이가 유의하다고 하자.
• 그러면, 한 어레이에 20K (2만 개)의 gene이 있다고 할때, 0.01*20K = 200 개의 gene이 잠정적으로 잘못 call되게 된다. 왜냐면 20K의 gene은 워낙 개수가 많기 떄문에 우연히라도 p-value가 0.01보다 작을 확률이 있기 떄문이다.
• 따라서, 이러한 문제를 해결하기 위해 더 작은 p-value를 사용하여 FWER (Family-Wise Error Rate)와 FDR (False Discovery Rate)를 조절해야 한다.

1) FWER (Family-Wise Error Rate), Bonferroni correction

• 잘못된 test: P(적어도 하나의 hypothesis에서 false rejection) < $\alpha$
• P(no false rejection) > $1-\alpha$
• Bonferroni correction : FWER을 control하기 위해 m개의 hypothesis를 $\alpha$ 유의수준에서 test하는 경우에 각 test의 false rejection rate를 $\alpha/m$으로 사용하는 것.
• 예시: 만약 $\alpha = 0.05$이고, gene의 수 (hypothesis의 수)가 20K라면, Bonferroni correction을 이용한 새로운 p-value cutoff는 0.05/20K = 2.5E-6이다.
• 하지만, FWER는 Differential Expression Analysis에서 너무 보수적(conservative)인 경향이 있다. (아무것도 call되지 않는 상황)

2) False Discovery Rate (FDR = Adjusted p-value = Qvalue)

• V : type 1 에러 (False Positive)
• T : Type 2 에러 (False Negative)
• R : Call된 gene의 수
• FDR = V / R (FP / All called)
• FDR를 control한 다는 것은, 전체 call 된 gene중에 몇 %의 gene만이 잘못 call되었는지를 따져서, 그 비율을 조절한다.
• FDR은 FWER보다 덜 conservative하다.

참고) Benjamini and Hochberg, 1995

• FDR을 control하기 위한 방법을 제시한다., e.g. $FDR \leq \alpha^{*}$
• 각 test에 대한 p-value가 서로 독립이라고 가정하자.
• 모든 m개의 gene (x)에 대해, p-value를 rank한다 (y)
• $y = x\alpha^{*}/m$인 line을 그린다. $x = 1, ..., m$
• line보다 아래에 있는 gene만을 call한다.
• 1 gene인 경우 FDR = p-val이다.

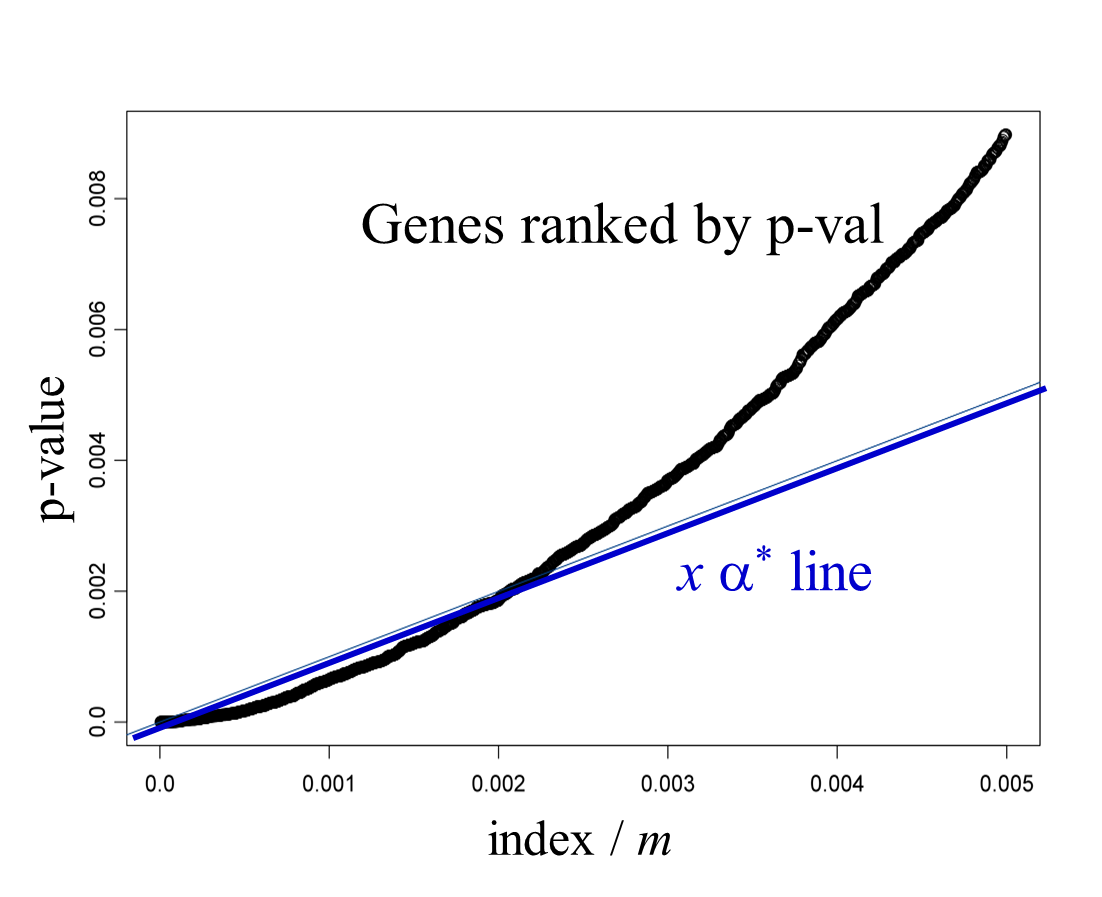
• 위의 그림에서 x축은 gene을 p-value에 따라 rank한 뒤 순서대로 order시킨 것이다. (m으로 나누어 지면서 0 ~ 1사이의 값으로 변경됨)
• 파란색 선은 FDR로 기울기가 커질수록 더 많은 gene이 call되게 된다. (파란선 아래의 gene을 call)
• FDR (파란색 선)은 test하는 gene이 많아질 수록 (x축이 오른쪽으로 갈 수록) 증가하는 것을 알 수 있다.

Q-value) by Storey & Tibshirani, PNAS, 2003

• 만약 differential expression analysis를 하는데, treatment와 control group간에 차이가 없으면 p-value의 distribution은 어떻게 생겼을까? -> 이런 경우 p-value는 uniform한 distribution을 가지게 된다.
• 반면 두 그룹간 유의한 차이가 있을 경우에 p-value의 분포는 다음 그림과 같다. 아래 그림은 3,170개의 p-value를 히스토그램으로 나타낸 것이다.
• 맨 위의 점선은 treatment와 control간에 gene expression의 차이가 없을 때를 나타낸다.
• (A 지역) 두 번째 점선은 FDR에 해당하는 선인데, 그림 설명을 보면 “The height of our estimate of the proportion of null p values”라고 되어있다. 즉 우연으로 발생한 값이라고 생각할 수 있다. 따라서, 두번째 점선 위의 값들이 (B 지역) 진짜로 유효한 p-value를 나타낸다고 볼 수 있다.

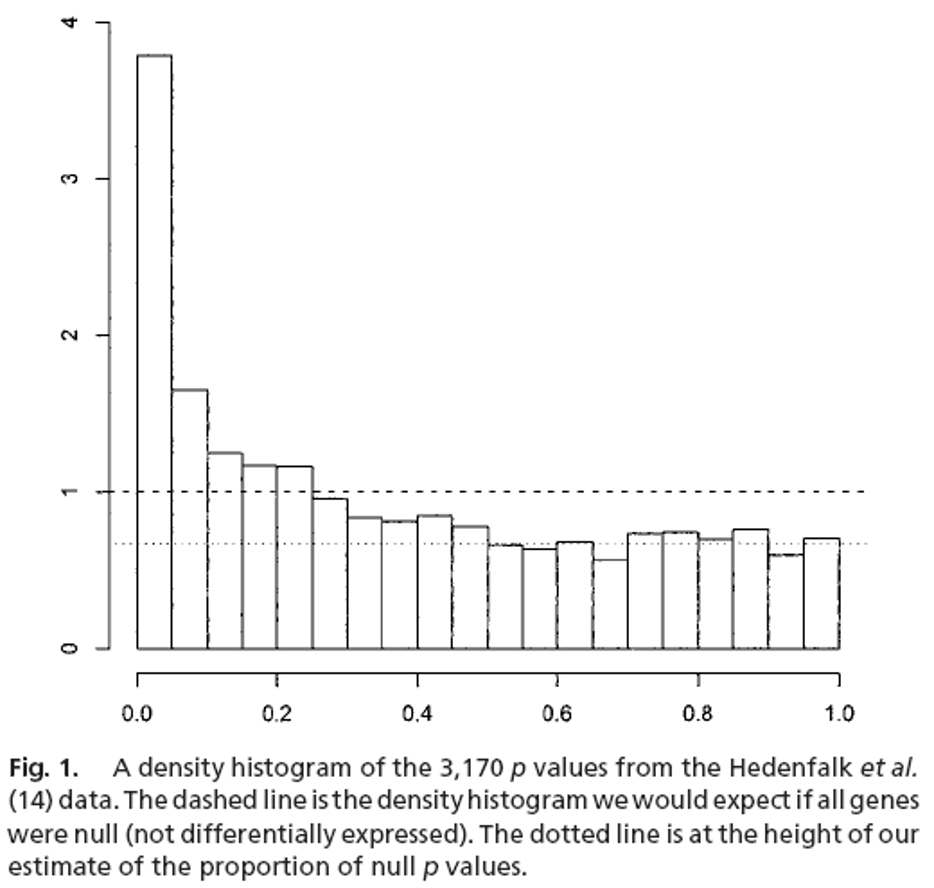
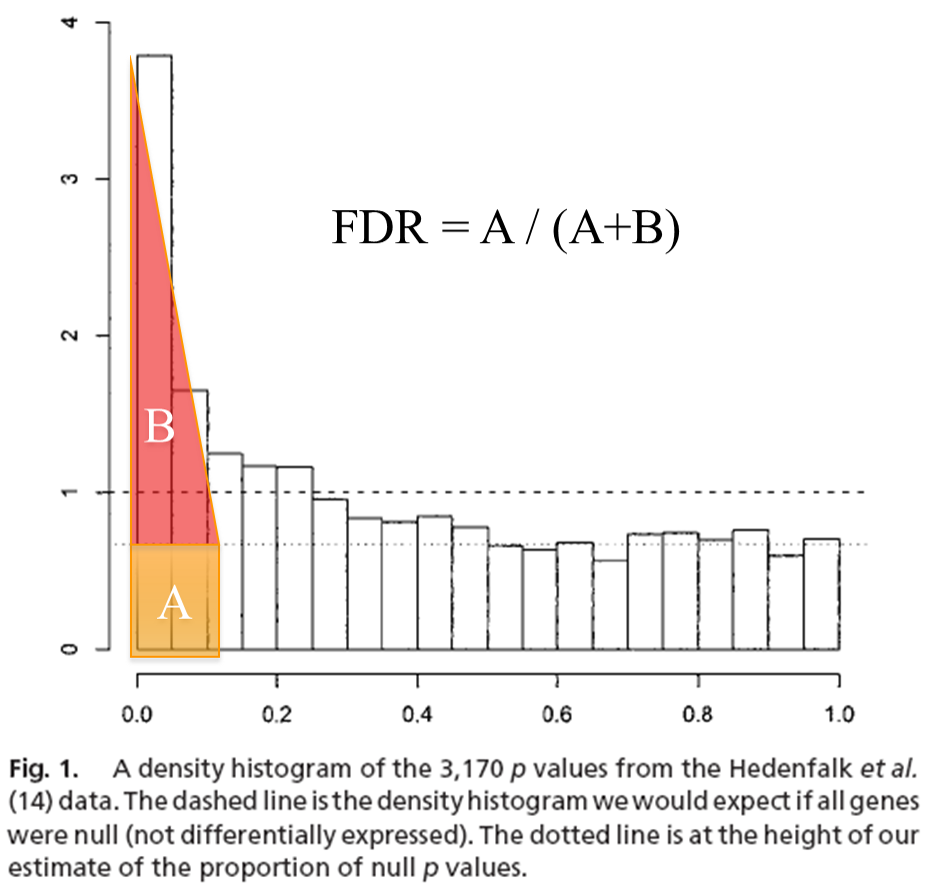
• 따라서, 분석을 시행할 때 FDR을 기준으로 하는 것이 좋다. (예: at FDR level 0.05) 그러면 p-value는 0.05보다 훨씬 더 작은 값을 가지게 된다.
• P-value와 FDR은 monotonic하다 : 모든 p-values는 그에 해당하는 FDR을 가진다. (FDR은 주로 p-value보다 큼 값을 가짐)
• 실제 주로 사용하는 FDR level: 1%, 5%, 10%를 사용함. (fold change로 filter한 값을 사용하기도 함.)
• FDR은 대략적인 signal / noise의 비를 줌으로써 실험의 quality를 추측할 수 있게 해준다.
• 보통 Differential expression analysis를 하면 500 ~ 2000개의 significant한 gene이 있게 된다.

Share this on →