Songwan's blog

By Goodfellow, Ian, et al. (2014).

Posted by : Songwan at Aug 31, 2019

Category : paperReview deepLearning

Note

이 포스팅은 논문 ( Goodfellow, Ian, et al. “Generative adversarial nets.” Advances in neural information processing systems. 2014.)을 리뷰한 글임을 알려드립니다.

Summary

이 논문은 generative model들을 adversarial process로 추정하는 새로운 방법을 제안하고 있다.

여기서 genearative model이란 우리말로는 생성모델이라고 하는데, ML wiki에 따르면, generative model은 분류에 쓰이는 모델으로, 각 분류 클래스의 분포를 likelihood, posterior등을 이용하여 학습하고 그 분포로부터 샘플을 생성하는 것이 목표이다. 반면, 분류(classification) 모델에는 discrimininative model (판별 모델)도 있는데, 이 모델은 decision boundary를 구축하는데 주안점을 둔다.

adversarial은 사전적으로는 “두 당사자가 적대 관계에 있는”이라는 의미이다. 이는 이후에 설명될 것 이지만, 두 가지 모델 G, D를 서로 경쟁시키면서 개선해나간다는 이유로 사용되었다.

논문에서는 동시에 두 가지 모델(G, D)을 trian하는 방법을 제시하는데, G는 generative model의 약자로써, 데이터의 분포를 추정하고, D는 discrimininative model의 약자로써, 샘플이 모델 G가 아닌 training data에서 왔을 확률을 추정한다.

G는 D가 실수를 할 확률 (즉, misclassification)을 최대화 시키는 방향으로 학습된다. 이 프레임워크는 두 명의 플레이어가 minimax를 하는 것과 동일하다.

Introduction

딥러닝 분야에서 지금까지는 discrimininative model이 주목받아 왔는데, 이는 이 모델이 backpropagation과 droupout알고리즘을 잘 사용하면 어느정도 높은 정확도를 보여주었기 때문이다. 반면, Deep generative model은 비교적 잘 주목받지 못했는데, 이는 복잡한 확률 계산과 MLE(우도함수)를 approximation하는 것이 어려웠고, 또 neural network의 선형적인 모델들을 generative한 관점에서 활용하기가 어려웠기 때문이다. 이 논문에서는, 이러한 generative model estimation의 어려움을 해소하기 위한 새로운 방법을 제시하고 있다.

저자가 제안하는 adversarial nets 프레임워크는 다음과 같다. 모델 G (generative model)와 모델 D (discrimininative model)이 계속 대립하면서 발전하는데, 우리의 경찰과 도둑 게임을 생각하면 이해하기가 쉽다. 도둑 역할을 하는 모델 G는 예측 분포로부터 training set과 유사한 (구분하기 어려운) 샘플을 생성해내고, 모델 D는 모델 G가 만들어 낸 training data를 분류 (구별) 한다. 이 두 모델의 성능이 좋아지면 좋아질 수록 모델 G는 training data와 더욱 더 유사한 분포를 만들 수 있고, 모델 D는 더 좋은 분류 성능을 가질 수 있다.

이러한 컨셉은 여러 optimization 분야에서 활용될 수 있으나, 저자는 이 논문에서 특별한 케이스만을 다루었다.

(조건 1) 모델 G는 다층 퍼셉트론간 random noise를 사용하여 전달한다고 가정한다.

(조건 2) 모델 D 또한 다층 퍼셉트론이다.

(조건 1) 과 (조건 2)가 모두 만족되었을 때를 adversarial nets라고 정의한다.

Adversarial nets는 다음과 같은 장점을 가진다.

적절한 backpropagation과 droupout을 통하여 D와 G를 잘 train할 수 있다.

Forward propagation만을 사용하여 모델 G에서 샘플을 생성할 수 있다.

이러한 과정에서 approximate inference나 Markov chain같은 복잡한 이론이 필요없다.

최근까지도, deep generative model에 관한 연구는 확률분포의 모수가 주어진 경우에 한해 집중되어왔다. 이러한 경우, maximum likelihood를 최대화 하는 방법으로 모델을 train할 수 있으며, 가장 유명한 예로는 deep Boltzmann machine이 있다. 이러한 모델들은 likelihood가 매우 다루기 어렵고, 따라서 gradient를 계산하는데 많은 approximation이 필요하다.

Restricted Boltzmann machine는 DNN이 backpropagation과정에서 신호가 약해지는 문제 (Vanishing gradient)를 initial weight를 효율적으로 정하는 방식으로 해결한다. 간단히 설명하자면 초기 weight를 forward와 backward의 차이를 최소화하는 값으로 지정한다. 이러한 network를 Deep Belief Nets (DBN)이라고 한다. 하지만 많은 numerical approximation이 필요하다.

(참고) Deep Boltzmann machine (DBM) : Salakhutdinov, Ruslan, and Geoffrey Hinton. “Deep boltzmann machines.” Artificial intelligence and statistics. 2009.

이러한 문제점을 해결하기 위해, generative machine이 고안되었다. Generative machine은 likelihood와 같은 것은 아니지만, 그래도 원하는 (desired) 분포로부터 샘플을 생성할 수 있게 해준다. 예를 들면, Generative stochastic networks는 numerical approximation 대신 backpropagation을 사용하여 모델을 훈련시킬수 있다. 이 논문에서는 Generative stochastic networks에서 사용된 Markov chain을 사용하지 않은 generative한 모델을 제안한다.

Adversarial Nets

이 프레임 워크는 모델 D와 G가 모두 multilayer perceptron일 때 가장 적용하기 쉽다. 다음과 같이 가정해보자.

$x$ : data

$p_g$ : generative distribution

$p_{\textbf{z}}(\textbf{z})$ : input noise variables( $\textbf{z}$ ) 의 prior

Genearative model의 분포 $p_g$ 를 데이터 $x$ 를 이용하여 학습시키기 위해, input noise 변수들인 $\textbf{z}$ 의 prior를 $p_{\textbf{z}}(\textbf{z})$ 라고 하자.

$G(\textbf{z}; \theta_g)$ : input noise 변수들인 $\textbf{z}$ 의 prior의 data space mapping

$G$ : multilayer perceptron (미분가능)

$\theta_g$ : multilayer perceptron parameter

$D(\textbf{x}; \theta_d)$ : single scalar(확률)를 반환하는 multilayer perceptron

$D(\textbf{x})$ : $\textbf{x}$ 가 $p_g$ 가 아닌 dataset에서 왔을 확률

$\theta_d$ : multilayer perceptron parameter

이제 모델 D를 G가 생성한 샘플과 training example에서 온 데이터를 분별할 확률을 최대화 하도록 훈련시킨다. Value function을 $V(G, D)$ 라고 할 때, 이는 two-player minimax game으로 생각 할 수 있다. 이를 수식으로 나타내면 다음과 같다. (여기서 $\mathbb{E}$ 는 기대값을 의미한다.)

$min_{G} max_{D} V(D, G) = \mathbb{E}_{\textbf{x} \sim p_{data}(x)}[logD(\textbf x)] + \mathbb{E}_{\textbf{z} \sim p_{\textbf{z}}(\textbf{z})}[log(1-D(G(\textbf z)))]$

위의 수식을 실제로 구현할 때에는 iterative, numerical한 방법을 사용해야 한다. D를 inner loop에서 optimize 하는 것은 computationally expensive하고, 유한한 데이터인 경우에는 오버피팅이 되어버릴 수 있다. 따라서, D를 일정 k step 만큼만 optimize하고, G를 1 step optimize하여 위의 문제를 해결한다. 이에 관한 더 자세한 내용은 논문의 Algorithm 1에 수록되어 있다. 또한, G를 $log(1-D(G(\textbf z)))$ 가 minimize되게 훈련시키는 것 대신에, G를 $logD(G(\textbf z))$ 가 maximize되게 훈련시키는 것이 초기 gradient가 더 잘 학습되도록 도와준다.

Generative adversarial nets의 단계

이 프레임워크를 좀더 자세한 설명을 위해 다음을 가정해보자.

분류기(파란색 점선) : discrimininative distribution (D)를 나타낸다.

생성모델의 분포(초록색 실선) : generative distribution ( $p_g$ )를 나타낸다.

트레이닝 데이터(검정색 점선) : data generating distribution ( $p_{\textbf{x}}$ )로부터 생선된 데이터(샘플)

$p_{\textbf{x}}$ 로 부터 샘플(검정색 점선)이 생성된다.

아래 도표는 Adversarial nets의 프레임워크를 보다 자세히 보여준다.

Generative adversarial nets는 훈련이 지속됨에 따라 discrimininative distribution (D)를 지속적으로 업데이트해 나간다. 분포 D가 $p_{\textbf{x}}$ 로부터 생성된 샘플과 $p_g$ 로부터 생성된 샘플을 잘 구분할 수 있도록 업데이트 된다.

$\textbf{x}$ : training data

$\textbf{z}$ : input noise variable (여기서는 uniform sample)

수평선 : $\textbf{z}$ ~uniform(수평선 domain)

mapping : $\textbf{x}$ = $G(\textbf{z})$ , G를 통해 high dimension인 $\textbf{z}$ 가 low dimension인 $p_g$ 차원으로 매핑됨.

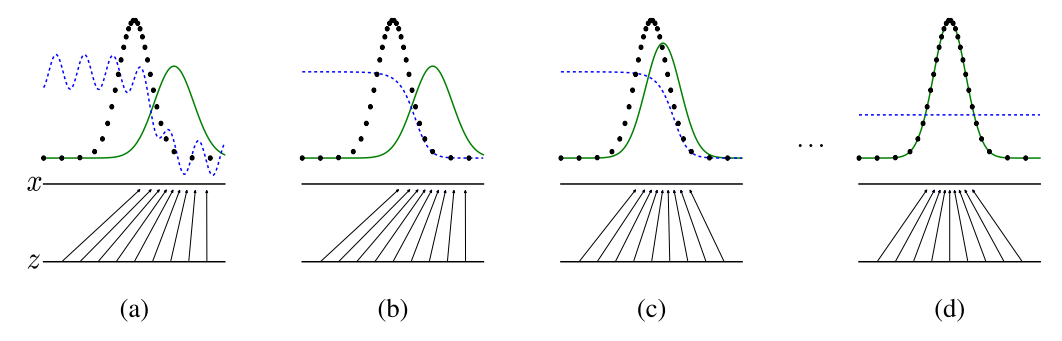
Generative adversarial nets는 (a)-(b)-(c)-(d)의 단계로 발전한다. 각 (a) ~ (d)에 대한 설명은 다음과 같다.

(a) adversarial pair인 분류모델과 생성모델의 훈련이 거의 converge 경우. 즉, $\approx p_{data}$ (데이터의 분포)이고 D가 부분적으로 정확한 성능을 보이는 분류기인 상태.

(b) 알고리즘 D의 inner loop가 생성 샘플과 실제 데이터를 구분하도록 훈련되었고, 그 결과 $D^{*}(\textbf{x})$ 는 다음으로 수렴하였다. (원문의 Proposition 1에 의해 D*는 D의 optimal이다. )

$D^*(\textbf{x}) = \frac{p_{data}(\textbf{x})}{p_{data}(\textbf{x})+p_{g}(\textbf{x})}$

(c) G가 업데이트 되면, D의 gradient는 $G(\textbf{z})$ (화살표들)가 training data로 분류가 될 확률이 더 높은 지역(범위)로 이동되게 한다. 즉 (b)와 (c)를 비교해보면 화살표들이 (b)에서는 $p_g$ 에 더 몰려있는 걸 알 수 있지만, (c)에서는 training data의 분포인 $p_{\textbf{x}}$ 에 더 몰려있는 것을 알 수 있다.

(d) 몇 차례 training step이 끝난후 만약 G와 D가 충분한 capcacity가 있다면, = $p_{data}$ 인 지점 (global optimum)까지 도달 할 수 있을 것이다. (즉, $D(\textbf{x}) = \frac{1}{2}$ )